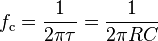Can your digital cable impact the sound of your system? Like most things, the answer is “maybe”… Reading some of the cable advertisements I see all kinds of claims. Some make no sense to me, such as “use of non-ferrous materials isolates your cable from the deleterious effects of the Earth’s magnetic field”. Hmmm… Some appear credible but describe effects that I have difficulty believing have any audible impact, such as “the polarizing voltage reduces the effect of random cable charges”. True, a d.c. offset on a cable can help reduce the impact of trapped charge in the insulation, but these charges are typically a problem for signals on the order of microvolts (1 uV = 0.000001 V) or less. Not a problem in an audio system even for the analog signals (1 uV is 120 dB below a 1 V signal), let alone the digital signals. But, there are things that matter and might cause problems in our systems.
Previously we discussed how improper terminations can cause reflections that can corrupt a digital signal. This can cause jitter, i.e. time varying edges, that are dependent upon the signal, which is really an analog signal from which we extract digital data (bits). As was discussed, this is rarely a concern for the digital system as signal recovery circuits can reject a large amount of jitter and extensive error correction makes bit errors practically unknown. The problem is when the clock extracted from the signal (bit stream) is directly used as the clock for a DAC. The DAC will pass any time-varying clock edges to the output just as if the signal was varying in time. It has no way of knowing the clock has moved, and the result is output jitter. Big enough variation and we can hear it as distortion, a rise in the noise floor, or both.
One thing all cables have is limited bandwidth. Poorly-designed cables, or even well-designed cables that are very long, may limit the signal bandwidth. This causes signal-dependent jitter. How? Look at the figure below showing an ideal bit stream and after band limiting. I used a 1 us bit period (unit interval) for convenience; this is a little less than half the rate of a CD’s bit stream.
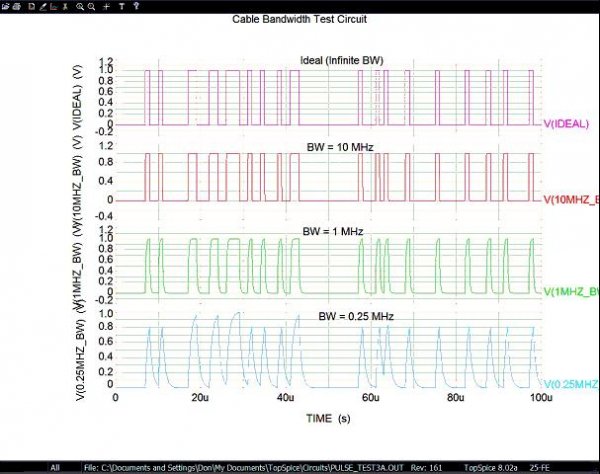
There is almost no difference between the ideal and 10 MHz cases. Since 10 MHz is well above 1/1 us = 1 MHz we see hardly any change. Dropping to 1 MHz, some rounding of the signal has occurred, and at 0.25 MHz we see that rapid bit transitions (rapidly alternating 1’s and 0’s) no longer reach full-scale output. Looking closely you can see that the period between center crossings (when the signal crosses the 0.5 V level) changes depending upon how many 1’s or 0’s are in a row. With a number of bits in a row at the same level, the signal has time to reach full-scale (0 or 1). When the bits change more quickly, the signal does not fully reach 1 or 0. As a result, the slope is a little different, and the center-crossing is shifted slightly in time. This is signal-dependent jitter.
A better way to see this is to “map” all the unit-intervals on top of each other. That is, take the first 1 us unit interval (bit period) and plot it, then shift the next 1 us to the left so that it lies on top of the first, and so forth. This “folds” all the bit periods into the space of a single unit interval to create an eye diagram (because it looks sort of like an eye). See the next figure.
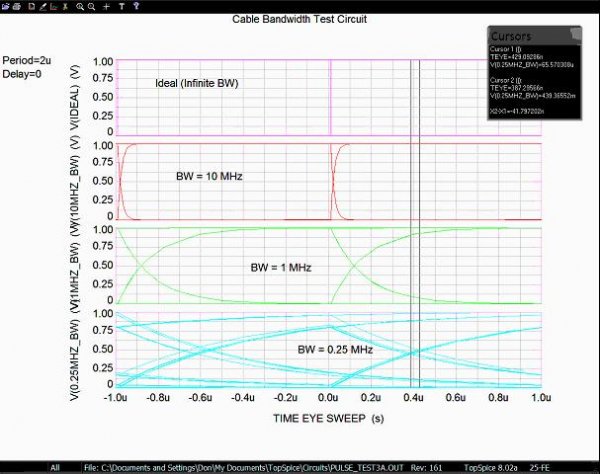
The top (ideal) plot shows a wide-open eye with “perfect” edges. As the bandwidth drops to 10 MHz we see the edges now curve somewhat, but there is effectively no jitter seen. That is, the lines cross at the center at one point, no “spreading”. With 1 MHz bandwidth the slower (curving) edges are very obvious, but still the crossing happens essentially at a single point. In fact jitter has increased but it is not really visible.
At 0.25 MHz there is noticeable jitter, over 41 ns peak-to-peak. That is, the center crossings no longer fall at a single point in time, but vary over about 41 ns in time. Why? Look at the 1 MHz plot and notice when the signal changes, rising or falling, it still (barely) manages to reach the top or bottom before the next crossing begins. That is, the bits reach full-scale before the end of the 1 us unit interval (bit period). However, with only 0.25 MHz bandwidth, if the bits change quickly there is not time for the preceding bit to reach full-scale before it begins to change again. You can see this in the eye where the signal starts to fall (or rise) before it reaches the top or bottom (1 V or 0 V) of the plot. This shifts the time it crosses the center (threshold). If the DAC’s clock recovery circuit does not completely reject this change, the clock period will vary with the signal, and we get jitter that causes distortion at the output of our DAC.
How bad this sounds depends upon just how much bandwidth your (digital) cable has (a function of its design and length) and how well the clock recovery circuit rejects the jitter. It is impossible to reject all jitter from the clock recovered from the bit stream, but a good design can reduce it significantly. An asynchronous system that isolates the output clock from the input clock can essentially eliminate this jitter source.
HTH - Don
Previously we discussed how improper terminations can cause reflections that can corrupt a digital signal. This can cause jitter, i.e. time varying edges, that are dependent upon the signal, which is really an analog signal from which we extract digital data (bits). As was discussed, this is rarely a concern for the digital system as signal recovery circuits can reject a large amount of jitter and extensive error correction makes bit errors practically unknown. The problem is when the clock extracted from the signal (bit stream) is directly used as the clock for a DAC. The DAC will pass any time-varying clock edges to the output just as if the signal was varying in time. It has no way of knowing the clock has moved, and the result is output jitter. Big enough variation and we can hear it as distortion, a rise in the noise floor, or both.
One thing all cables have is limited bandwidth. Poorly-designed cables, or even well-designed cables that are very long, may limit the signal bandwidth. This causes signal-dependent jitter. How? Look at the figure below showing an ideal bit stream and after band limiting. I used a 1 us bit period (unit interval) for convenience; this is a little less than half the rate of a CD’s bit stream.

There is almost no difference between the ideal and 10 MHz cases. Since 10 MHz is well above 1/1 us = 1 MHz we see hardly any change. Dropping to 1 MHz, some rounding of the signal has occurred, and at 0.25 MHz we see that rapid bit transitions (rapidly alternating 1’s and 0’s) no longer reach full-scale output. Looking closely you can see that the period between center crossings (when the signal crosses the 0.5 V level) changes depending upon how many 1’s or 0’s are in a row. With a number of bits in a row at the same level, the signal has time to reach full-scale (0 or 1). When the bits change more quickly, the signal does not fully reach 1 or 0. As a result, the slope is a little different, and the center-crossing is shifted slightly in time. This is signal-dependent jitter.
A better way to see this is to “map” all the unit-intervals on top of each other. That is, take the first 1 us unit interval (bit period) and plot it, then shift the next 1 us to the left so that it lies on top of the first, and so forth. This “folds” all the bit periods into the space of a single unit interval to create an eye diagram (because it looks sort of like an eye). See the next figure.

The top (ideal) plot shows a wide-open eye with “perfect” edges. As the bandwidth drops to 10 MHz we see the edges now curve somewhat, but there is effectively no jitter seen. That is, the lines cross at the center at one point, no “spreading”. With 1 MHz bandwidth the slower (curving) edges are very obvious, but still the crossing happens essentially at a single point. In fact jitter has increased but it is not really visible.
At 0.25 MHz there is noticeable jitter, over 41 ns peak-to-peak. That is, the center crossings no longer fall at a single point in time, but vary over about 41 ns in time. Why? Look at the 1 MHz plot and notice when the signal changes, rising or falling, it still (barely) manages to reach the top or bottom before the next crossing begins. That is, the bits reach full-scale before the end of the 1 us unit interval (bit period). However, with only 0.25 MHz bandwidth, if the bits change quickly there is not time for the preceding bit to reach full-scale before it begins to change again. You can see this in the eye where the signal starts to fall (or rise) before it reaches the top or bottom (1 V or 0 V) of the plot. This shifts the time it crosses the center (threshold). If the DAC’s clock recovery circuit does not completely reject this change, the clock period will vary with the signal, and we get jitter that causes distortion at the output of our DAC.
How bad this sounds depends upon just how much bandwidth your (digital) cable has (a function of its design and length) and how well the clock recovery circuit rejects the jitter. It is impossible to reject all jitter from the clock recovered from the bit stream, but a good design can reduce it significantly. An asynchronous system that isolates the output clock from the input clock can essentially eliminate this jitter source.
HTH - Don
Last edited: