Actually that's not how it manifests. Here's the FM theory: there should be two sidebands in your graph around the music tone, + and - beat frequencies. An A440 flute tone with a 0.1% flutter of 60Hz and 120Hz (typical with AC cogging motors) will have sidetones of 500 660 and also 380 and 320 at about -60db. Which is not healthy, nor is it easily masked - the first recording we noticed this on was a piano/clarinet duet and the beats in the clarinet were quite obvious, after hearing them absent... It's a ring modulation.
I didn't say FM creates a single sideband but rather, expanding on how maksing works in general. As to your point, I wrote:
"My note was relative to the common manifestation of speed variation which is in the very low frequencies of a few hertz where its amount can be very large yet surprisingly inaudible as distortion in the way we think about it. To the extent the system has high frequency variations of the rates you mention then yes, it will occur at higher frequencies and masking is not as helpful -- just like in our digital systems. That was the point of my first paragraph you quoted in how tape transports had changed in the later years and introduced high frequency variations."
The examples you cite are clearly more than a few Hertz and agree with my statement and explanation of masking and how it is not as effective there. So please don't post again saying we disagree

.
The reason for my original post was that often analog systems are compared to digital and people wonder why we worry about picoseconds of jitter where far larger amounts of it in analog systems is not talked about as being problematic. Much of the reason for that is masking. I wrote a much longer post explaining the difference on another forum as *it relates to very low frequency wow and flutter*. Here it is:
----------------------------------------------------
OK, some free time to reply to Terry's request on the relationship between Flutter and Jitter.
Let me start this with saying I have not studied the perceptual effects of flutter in analog equipment. It has not been an area of interest for me in the past and likely won't be in the future. While I am hoping to add fair bit of data to this discussion, my goal is not to quantify what flutter sounds like but rather, whether its concepts apply to jitter in digital systems. In that sense, some of this reply is open-ended and I welcome others' feedback on what it means as a complete picture.
With that out of the way, let me frame the question as I understand it. The thread again started with me saying very low frequency (50 to 100 Hz) jitter is not as audible as high frequency ones. Arny objected and went on to cite references regarding flutter instead, and how as its frequencies increase, the opposite is true. Unfortunately his references are to papers not available to general public and hence I have not read them. Regardless, I am going to take his word for it and attempt to analyze the situation.
FM Modulation
Arny has correctly stated that both jitter and flutter are Frequency Modulation or FM for short (if this were an advanced topic, we would talk about jitter also being a form of phase modulation but that distinction is not material here). What is frequency modulation? It simply means you take a signal -- called a carrier (Fc) -- and change its pitch or frequency proportional to another signal (Fm). The terminology makes sense in the context of RF transmissions but not so much in our audio world. To clarify then, our "carrier" in this discussion is our music. The modulator signal (Fm) is flutter or jitter. It is the thing that forces the change in frequency of our music tones.
As an example of FM modulation, if I have a 1 KHz tone and a 2 Hz flutter, the 1 KHz tone changes in frequency every half a second and keeps repeating. You will hear this as "WOW" which is the name of flutter when its frequency is very low. It kind of sounds like wow wow wow.
As an aside since complex sounds like music can be decomposed into a series of sine waves, we have countless carriers, each being modulated by the flutter/jitter. So even though we usually show a single tone as the carrier in demonstrations of jitter effect, our music represents many carriers and hence the real picture is far more complex (and hence has more distortion products). But we digress.
I hope everything is clear so far because from here on, it is going to get complicated

.
Perceptual Effects and Modulation Index
To know the effect of Frequency Modulation, we need to look at the signal in frequency domain. In time domain we simply see the carrier shrinking and expanding with the modulator which is uninteresting as far as deducing distortion products. In frequency domain, an entirely different picture exists where we see new frequencies created that have nothing to do with the original signal. The nature of these new frequencies/distortion products depend on a key parameter called the "modulation index:"
Modulation index = peak frequency deviation / Fm
The denominator is the flutter or jitter bandwidth which in case of simple simulations of a single tone, is equal to the frequency of that tone. So this part is easy to understand.
The numerator is the maximum change in the carrier (or music signal) frequency. What determines this is the *amplitude* of the modulation signal. After all, that is what frequency modulation is. The louder the modulation signal, the more the carrier shifts in frequency. And the fainter it is, the less it does that.
The mathematics tells us that as the modulation index increases, the relevant distortion products multiply in number and relative amplitude (in reality they are always there but the higher order values are so close to zero as to not matter in cases of lower modulation index). In case you are curious, the representation of the distortion products is the Bessel functions. Going on a limb and assuming you don't know what a Bessel function looks like, here is a great visualization which shows what happens as we go from very low modulation (called narrowband FM) to very high (wideband FM):
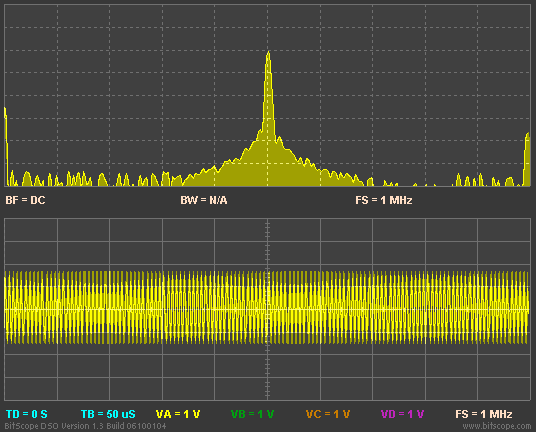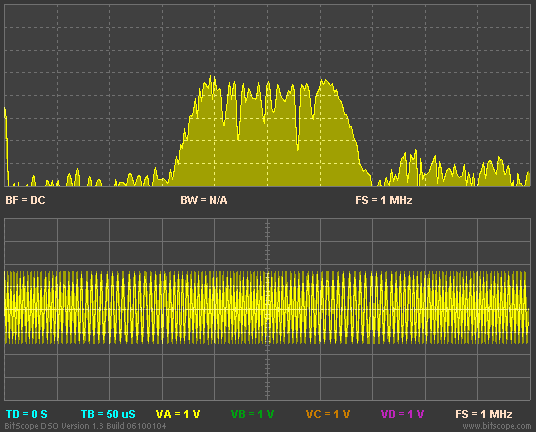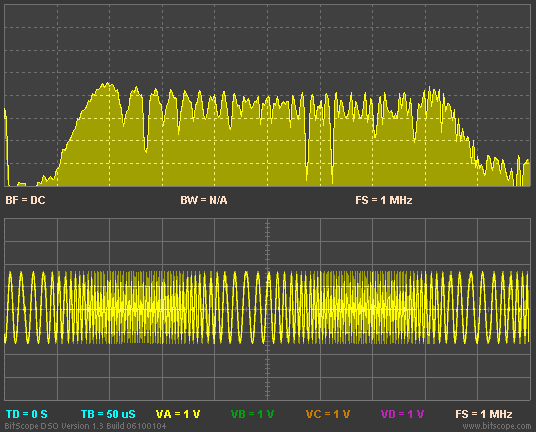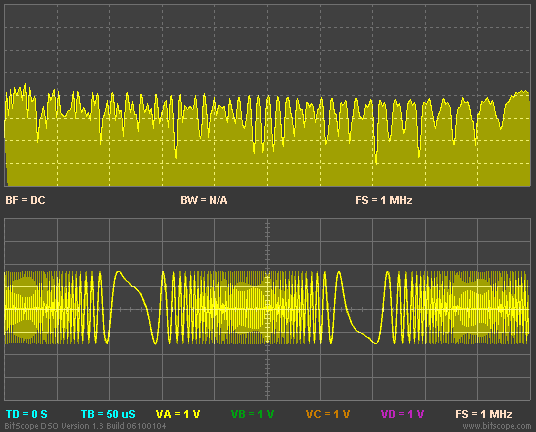
Notice our original tone in the middle as the animation starts (it is above the green letter "v"). We see that our simple tone quickly becomes a complex waveform including having its amplitude reduced and varied as modulation index rises. Indeed, this is the heart of "FM Synthesis" technology used to generate artificial sounds in music synthesizers and PC software alike. It is a simple way to create complex waveforms.
While the dancing graph is pretty it may still be hard to visualize what all of this sounds like. Fortunately I found a nice simulation from Columbia University that shows what happens as the modulation index goes from 6 to 0 (high to low), with a carrier of 100 Hz and a modulator frequency of 280 Hz:
http://music.columbia.edu/cmc/MusicA...r4/bell.fm.mp3
As the name indicates, one is able to simulate the sound of a bell with the mere action of changing the amplitude of the modulator! The ear is not hearing the tone change at the beginning but an entirely different sound due to combination of the original tone plus all of the new distortion products. All the while, both the carrier and modulator frequency stay constant. The only thing changing is the amplitude of the modulator. Yet we don't perceive that as an increase in distortion after some point but a wholesale change in sound.
Modulation Index effect on Flutter and Jitter
Recall the mathematics of jitter from Dunn's seminal paper that I have often used to show how we drive the jitter spectrum and its amplitude. Here I have reproduced it with a circle to highlight something important:
He starts with the textbook definition of FM modulation which is to change the frequency of the carrier. He then takes a massive shortcut without which, the solution would have been orders of magnitude harder and result in the aforementioned Bessel functions. That shortcut comes courtesy of considering that jitter amplitude in digital systems is usually very weak relative to the original signal. Recall for example the example I used where jitter was at -80db.
When we do that, we throw out a bunch of terms out of the equation and are left with the solution that there are only two sidebands of interest with their frequency being +- jitter frequency as I explained in my last long post. Dunn then calls this outcome "AM modulation" since that is the result of amplitude modulation. In reality, we still have an FM modulator but our modulation index is so low that all the rest of the sidebands are down to zero and hence of no interest. This is what the dynamic simulation above shows the minute the cycle starts -- the original tone plus two sidebands.
Now it is time to look at flutter. As Arny has correctly put it, the amplitude of flutter in analog world as a modulation signal is quite large relative to jitter assumption above. Here is his positioning:
arnyk said:
The jitter due to wow and flutter in analog equipment at its best, is about 1 million times stronger than the jitter in the worst digital equipment. Another way to describe 1 million times stronger is to say that it is 60 dB greater.
Recall that modulation index is proportional to amplitude of the modulator and inversely proportional to its bandwidth/frequency. Therefore when it comes to flutter our numerator has shot way, way up. Therefore we are no longer living in the simple world that Dunn painted in digital domain. This means the other distortion terms do not go to zero and we have a full blow Bessel situation on our hand, if there is such a term

. The spectrum now has a ton of sidebands as the simulation shows with increasing modulation index.
The effect is magnified in other ways. Assume someone is performing audibility tests for flutter. Naturally they start with very low frequencies such as 0.5 Hz to say 20 Hz. Because the numbers are so small, they (a) make the modulation index bigger since it is in the denominator. But further, as you vary them, their effect on the modulation index is quite a bit bigger. For example, as you go from 1 Hz to 4 Hz, the change in modulation index is 4:1. That large change in modulation index radically modifies the resulting audio spectrum and hence level of audibility.
Such is not the case in digital/jitter. For one, the frequencies of interest are not that low but more importantly, the numerator for modulation index is so much smaller that changing the modulator frequency does not impact it that much. We may go from 0.01 to .02 modulation index whereas flutter may go from 2 to 4. The former does not create new sidebands whereas the latter certainly does. But further the creation of sidebands also changes the amplitude of the carrier itself. So you get hit coming and going as modulation index changes. Again you can see this in the visualization as the center tone changes its amplitude in unison with higher modulation indices.
Frequency Unmasking
As much as I have talked about frequency masking, it is important to understand that there are cases where distortion products become unmasked due to another factor and hence, potentially become audible. Such is the case with modulation index. Look at the two snapshots of our first visualization at the beginning (very low modulation index) and end (high modulation index):
Notice two things. First, the amplitude of the carrier or in our case, the original music tone has gotten attenuated. And second, the bandwidth of the sidebands per earlier description has been hugely widened. So not only the masking shadow around the primary music tone has much less amplitude due to shrunk strength of the carrier but that there are now components easily going past the skirts of masking. No amount of masking will cover the second scenario of higher modulation index.
Here is another visualization on the same theme:
Look at the modulation index 2 where the carrier is so much less strong than the sidebands. Clearly no masking occurs for the strongest sidebands next to the carrier. Only marginal effect exists for the third sidebands if any.
Depending on the carrier, modulation frequency and severity of modulation index, it is possible to actually fully suppress our original music tone and be left with nothing but distortion products! In that situation, there is no masking whatsoever from the music itself (although the sidebands mask each other by varying degrees).
So let's say our flutter frequency was the same as line frequency at 100 Hz. Unlike jitter, we have more sidebands due to high modulation index coupled with reduced power of our original tone. The sidebands may extend for many multiples of 100 Hz (including some inharmanics). So any masking is going to only cover part of the distortion spectrum and some distortion will lilkely leak through.
Again, none of this at play with jitter because the modulation index is so much lower and hence, we have a full amplitude carrier (music), and only two sidebands of much lower amplitude being strongly masked in the case of low frequency jitter.
Wow and Flutter Perceptual Model
As I noted, my goal is not to convince you of audible artifacts of Wow and Flutter. But let me share some data that I do have since the topic has been so much discussed by Arny.
The first point is that when we perform Wow and Flutter measurements, we use a standardized frequency weighting. Arny noted the same in his later posts (drawing from the Wikipedia article):
arnyk said:
I double checked the reference, and the quote from Villchur and Allison was correct and in context. It is also incorrect in the light of a number of later references including Zwicker and Fastel etc.
Since it shows weighting designed to correspond to the sensitivity of the human ear, it is showing an attenuation of low frequency noise. The human ear essentially attenuates its sensivity to FM noise at low frequencies.
The curve of course does NOT agree with what started this entire debate as Arny corrects himself above. He originally said that as the frequencies of flutter increased, audibility kept declining. The CCIR/DIN/IEC curve above clearly articulates a different situation where there is a peak at 4 Hz (i.e. most annoying).
Now let's refer to another slide from the FHG presentation I originally cited which actually builds on Arny's reference book on perceptual models as footnoted:
As you see in chart (c) for FM modulation, there is a sensitivity peak at 4 Hz which is hypothesized as being the case due to human evolution of trying to understand speech which itself is a manifestation of temporal masking (see the slide I post earlier). This nicely agrees with the industry recommendation of paying more attention to 4Hz as the most critical frequency for wow and flutter.
Small and Big Signal Theory
The Electrical Engineers reading this are familiar with analog circuit design where we have the concept of "small signal" and "large signal" analysis. It would be deadly to take small signal rules and apply them to large signal usage of the circuit. The same is in play here. Just because "FM modulation" is used in both jitter and Flutter, we don't get to blindly apply the rules of one to the other. The amplitude of the modulation index radically changes the nature of the situation and its analysis.
Orthogonality of Jitter and Flutter Distortions
A key consideration here is that jitter has a characteristic that flutter never has: data dependency. A tape recorder wow and flutter does not change based on what is being recorded or played. The variations come from mechanical aspects of the machine. The electrical signal driving the head makes no difference. Not so with jitter. Jitter can be induced because one transmits certain data pattern.
Recall the cable example I gave earlier. Such a modulator is not periodic and can cause distortion products not modeled by the above analysis. And it certainly is not anything predicted from flutter world.
Further, digital systems MUST be bandwidth limited to half of their sampling frequency. Bad things happen when you don't do that. Jitter adds sidebands that are at +-frequency of jitter relative to music spectrum. It is very easy to imagine cases where the addition of jitter to music pushes us past the maximum allowable bandwidth. When you do that in digital systems, the new frequencies fold back to into the audio band. This will have an entirely different effect than in analog system where it either sits in ultrasonic band or gets filtered out.
As an example, an 8 KHz jiter tone added to 21 Khz creates an upper sideband at 29 Khz. In CD with bandwidth of 22 KHz, that folds back to 14 Khz due to us exceeding the system bandwidth and resulting aliasing. Therefore we go from a 21 Khz signal which most likely was not audible to a 14 Khz tone which may very well be. In analog world, we just have a 29 Khz tone which is an entirely different animal than 14 Khz. Yes, I made up this example on purpose

. But since you have no control over your music frequency content and that of jitter, it certainly can be one of the outcomes.
Summary
1.Yes, Flutter and Jitter are forms of FM modulation. For the reasons that it hurts differently if you got hit by a golf ball in the head than a basketball

, just because the roots are the same, it doesn't mean perceptual effects are the same. Flutter amplitude is considerably higher and hence, creates a different situation.
2.Modulation index determines the bandwidth of an FM signal and flutter by definition has a wider distortion spectrum than jitter.
3.While frequency masking is alive and well at all times, its effect can sharply be reduced based on modulation index and with it, allowing distortions to be heard that would not otherwise be as audible.
4.Wow and Flutter standardized curves have a 4 Hz maximum importance with the amount dropping on both sides of that center frequency. Therefore Arny's original thesis is invalidated that as flutter frequencies increase, there is a downward slope in audibility of the distortion. He has acknowledged the same although it doesn't look like anyone picked up on that.
5.As I noted many pages back from the well written and simple presentation by FHG, the explanation of 4 Hz peak appears to be very related to temporal masking where the distance between fluctuations determines audibility.
6.There are cases such as jitter aliasing and data dependent jitter that simply have no analog in flutter. So as much as the levels of jitter can be lower than flutter, it can manifest itself in ways flutter cannot. So one has to be very careful in drawing parallels here. (There are other considerations here that I am not covering here just yet.)
----------------------------------








