Jitter 102C

[DonH50]

<continued from Jitter 102B>

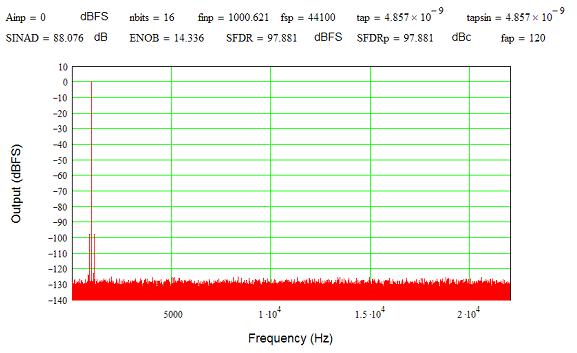
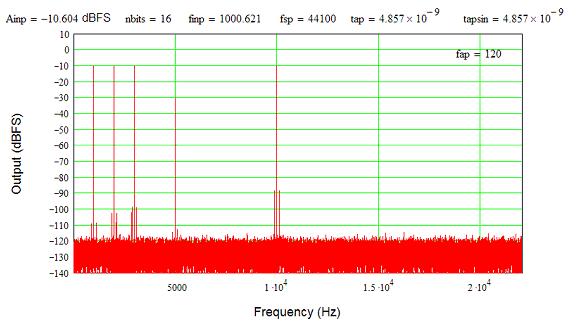
An interesting experiment is to throw in a deterministic term not related to the signal. Below is a plot with the jitter modulated by a 120 Hz signal, such as would come from a typical full-wave power supply, again at the 1-lsb level. Note the ENOB did not change significantly, but now there is a pair of spurs around the 1 kHz signal. Other frequencies, and more complex combinations of deterministic jitter, can generate a series of tones that are not related to the signal. This is important because we can hear non-harmonic distortion much more readily than harmonic distortion.



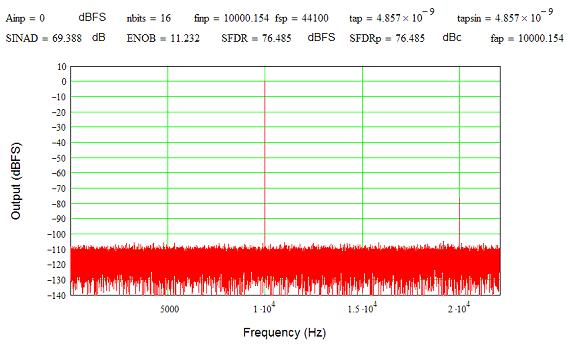
Repeating the plot at 10 kHz with 1 lsb of 10 kHz signal injected puts a spur at 20 kHz at the same level as in the 1 kHz plot, just like the first trials. Using the 1 kHz jitter level as modulated by the 10 kHz signal yields a fairly high (about -76 dBFS) distortion term.



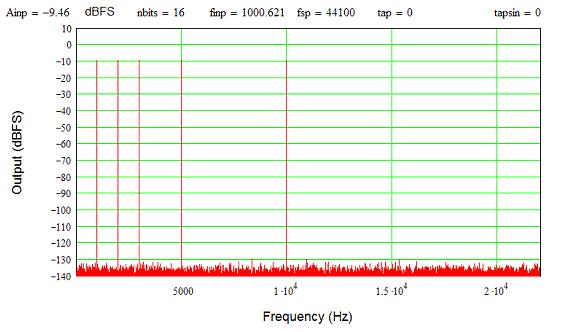
One last series of trials… Here’s a plot using five input tones (1, 2, 3, 5, and 10 kHz) without jitter. Notice the tones are all about 10 dB down; this is because when the all add up (in phase), they drive the DAC to full-scale, even though the average is -10 dB per tone. Music is much more complex thus average values are often -20 dBFS or less to ensure the output doesn’t clip (and sound very, very bad). This eats into your dynamic range pretty quickly, and helps explain why what appears to be low jitter can start to impact the ‘real world” noise floor. It also helps explain why recording systems and studios really like using 24 bits; that extra headroom is a boon when working with everything in the mix before the amplitudes are matched and the signal made to fit back into 16 bits for your CDs.



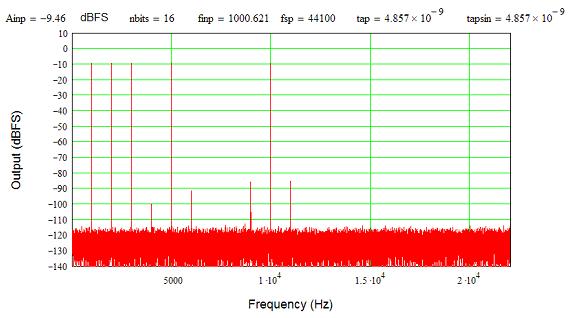
Here are those same tones but with 5 ns (1 lsb at 1 kHz again) of jitter added, along with 1 lsb of the 1 kHz tone added to the jitter. Note the multiple tones added as the deterministic jitter mixes with the other tones through the sampling process. The effective SFDR is now only about 75 dB from peak signal to peak spur…



My last example is those same five tones, but with the 5 kHz tone reduced 20 dB (about ¼ volume) to emulate what might happen in (very simple) music. I moved the deterministic jitter to 120 Hz, though still at 5 ns (1 lsb at 1 kHz). The distortion spurs are much more numerous and only about 60 dB down (worst-case) from the reduced 5 kHz tone. Would you hear this? I don’t know, but probably not. However, it is clear that as we move toward more complex signals like music, and correspondingly more complex and realistic jitter, we are heading toward something that could be readily audible.



Hopefully this has given you a picture of what jitter can do, and a flavor for the real-world impact it might have. My goal was not a realistic, musical example (readily done but the plots would be very messy), but rather something that helps clearly show what jitter does to DAC performance. Thus, I have not used complicated signals so (hopefully) it is easy to see what happens when jitter is added.

Enjoy! - Don

 

[Phelonious Ponk]

So what is the English language version? In a decent quality DAC where would we expect the artifacts to land relative to the signal? Is it likely to be audible in a real-world listening situation, even with a pretty modest DAC?

P

 

[DonH50]

You know I'm an engineer, right? English is a second language to me...

You'll get lots of debate on all of that... I am certainly not an expert on all the DACs available today and their specs, nor what people consider "decent" or "audible", and cannot claim to have golden ears, but here are my guesses:

1. The artifacts are related to signal content and so can (and will) be spread throughout the spectrum by random jitter. Deterministic jitter related to the signal in music will generate spurs related to the musical signal so "where" can get complicated. They will appear across the band, but in more discrete tones and at higher levels than equivalent power random jitter.

2. I would guess random jitter would be inaudible in most systems (Amir and some others may take issue with that, but I did say "guess"). Deterministic jitter, well, I can't say for sure as I do not know enough about jitter levels in average systems. I suspect it has broached the audible barrier in many systems due to coupling and pattern noise corrupting the DAC's clock. As you can see, a little deterministic jitter has a much bigger impact than the same "level" as random jitter, in part because the energy gets concentrated at one (or a series of) discrete frequency(ies) instead of being all spread out. We are sensitive to non-harmonic tones, and that's what deterministic jitter can generate. Whether you can hear it in music, I don't know.

I had in mind to run some square-wave trials to see if I could detect edge corruption, but this got time-consuming, I have work to do, and my spare time for the next couple of weeks needs to be spent re-acquainting myself with my neglected smaller horns before the philharmonic's season starts in a couple of weeks (practice, practice, practice).

In this area, I'm just sticking with the facts, sir or ma'am, and unfortunately (or not, actually) I think the debate will rage on. At least people may get a flavor for what we're talking about.

HTH - Don

 

[amirm]

As Don says, the science doesn't say what is audible. But rather, teaches one the complex nature of jitter (i.e. it is not one number). And possibly what to listen for in searching for it. The latter is important to deal with the claims of "I don't here it therefore it is not audible." By understanding the science and different ways jitter could manifest itself, then you have a shot at learning to hear it.

I do agree with Don that random jitter is mostly benign at levels in good audio equipment. It is the other types of jitter which are cause for worry. Unfortunately, jitter tends to be a system problem encompassing multiple pieces of equipment so reviews of one gear won't tell you for sure what your jitter situation might be. Two PCs for example driving a DAC could represent two very different situations as far as the DAC is concerned.

My view on jitter is simple: I want a digital system which resolves the most bits it possibly can within the budgets I have. In this forum we strive for the best and I don't see how the best DAC can be one that only resolves 14 bits when member routinely talk about high res downloads of 24 bits and such.

PS Thanks Don for writing all of these articles. I am sure it was a lot of work! You certainly have gone beyond the call of duty with the graphs and simulations.

 

[Steve williams]

I have a new hero now Amir.

Don your work to do all this is greatly appreciated. Now as P said, give us the English version..

 

[FrantzM]

Hi

I don't know for sure if jitter is audible or not. I canonly say based on what I have read and Don excellent work to present an otherwise complex subject in sumple fashion that we have even more to learn about jitter manifestation in term of audible artifacts.
It doesn't seem we know enough at this point in time. I have no vested interest one way or the other. Declaring however that all CD/Digital players sound the same or that jitter is inaudible is not a wise option.

 

[DonH50]

Thanks guys!

Frantz, using absolutes is never wise...

 

[Phelonious Ponk]

Thanks guys!

Frantz, using absolutes is never wise...

Absolutely.

Thanks Frantz. No, I didn't know you were an engineer until I read that post, but that did make it obvious.

P

 

[DonH50]

Design engineer, audiophile, musician, sometime teacher (college lecturer), father, husband, ex-cowboy (bareback), etc. "Specialization is for insects." - Heinlein

Checking the view count, this one has many more viewings than the first two in the series. Hmmm...

IMPORTANT: Jitter 102A, 102B, and 102C are a series of posts meant to be read in order. Actually, you should read Jitter 101 for background, then the three Jitter 102 threads. No fair skipping to the end! - Don

 

[Steve williams]

Don

All kidding aside, how about considering a Jitterr 103, to wit Jitter, A Crash Course For Dummies. I am just a lowly doctor whereas all you guys are EEs

 

[DonH50]

Hmmm... Thought you were kidding, Steve, sorry. Even my "simple" version needs simplifying, eh? I assumed a fairly basic technical understanding of waveforms and spectral plots, but I suppose that may not be something OB/GYNs routinely see... Why don't you drop me a note (PM, email, or just post here) with what you'd like to see/know and I'll see what I can do? I realize that sometimes knowing the question is the hard part, but at least that will get the ball rolling, and by starting that thread hopefully others can jump in and help me out (despite appearances, my time is limited, and about to become more so).

Actually, a better idea might be to start a "What Do You Want to Know?" thread that is essentially a list of questions; answers could be posted in separate threads as required.

Thinking - Don

p.s. Try this out: Digital systems sample signals. To correctly determine what we've got, we have to know exactly when we sampled since the signal is moving. That is, the two parameters that define the signal samples are the time and amplitude at any given sample. If we don't associate the signal's amplitude with the right time, that causes an error. Jitter is noise on the clock that makes the sampling time vary, generating errors. Random jitter, random errors, sound like noise. Deterministic jitter is related to something, and that makes distortion, i.e. specific tones in the output that we don't want to hear.