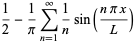Please repeat your specific question in a short, self-contained post.
Thanks, Tony, for your interest in helping. Groucho has already answered my question in post # 15; I am not sure if you agree with his answer and in any case, addtional observations are welcome.
In any case, here is my question in short form:
It has been suggested that any complex waveform can be synthesized from sinewaves, and thus according to the Nyquist theorem any music signal up to 20 kHz frequency can be perfectly represented by 44.1 kHz digital. Yet the following article by Chris Tham, "Exploring Digital Audio Myths and Reality Part 1" argues otherwise, that for example it does not apply to sawtooth waveforms:
http://www.audioholics.com/audio-technologies/exploring-digital-audio-myths-and-reality-part-1
Acoustic instruments that produce waveforms with, for example, saw-tooth like asymmetries, are trumpets, see the graphs in section 1.6.1 in the following article:
http://www.feilding.net/sfuad/musi3012-01/html/lectures/005_sound_IV.htm
So the question is: Is the 44.1 kHz standard indeed theoretically, on a technical level, insufficient when it comes to proper timbral resolution of acoustic instruments that produce complex, non-sine waveforms, and when it comes to the correct reproduction of odd non-sine waveforms (sawtooth, square) from synthesizers?