Multitones are steady state signals so I wouldn't expect them to highlight noise floor modulation. However, I have not done any testing to look for noise floor modulation. One could change the relative phase of the tones and thus change the crest factor of a multitone without changing its harmonic content. I wouldn't expect the noise level to change with crest factor but if it does, it would be worth investigating why.@AP, I've been talking about using multitone test signals as more appropriate & know AP scopes have some capabilities in this area - care to talk about that?
One thing I was interested in is using these multitone test signals to test for noise floor modulation - any ideas how this might be done?
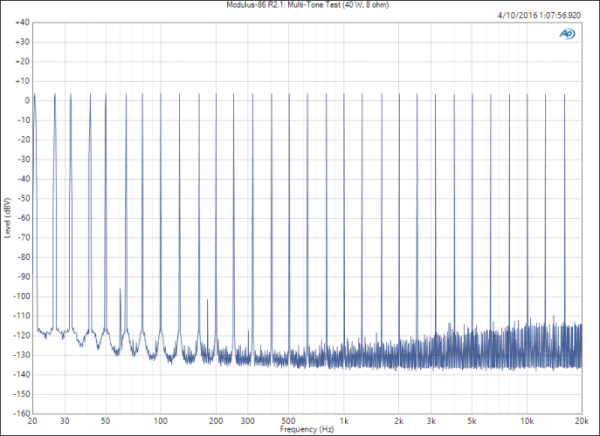
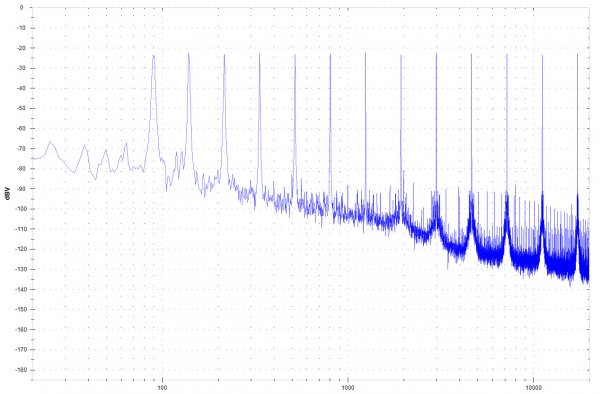
The AP multitone analysis uses a synchronous set of tones. This allows us to use a windowless FFT in order to get accurate results across a very wide bandwidth. We can extract frequency response, noise, phase, crosstalk and total distortion with one acquisition. The total distortion number is a summation of the harmonics of all the tones and the IM products of each tone mixed with the other. The more tones you have, the higher the TD will be. This makes correlating TD to standard THD and IMD measurements difficult.
ESS has given papers in the past about noise floor modulation in DACs. If I recall correctly, they measured this by simply changing DC levels between two states and recording the noise w.r.t. time. I couldn't find the paper and it was many years ago. My memory could be failing me.