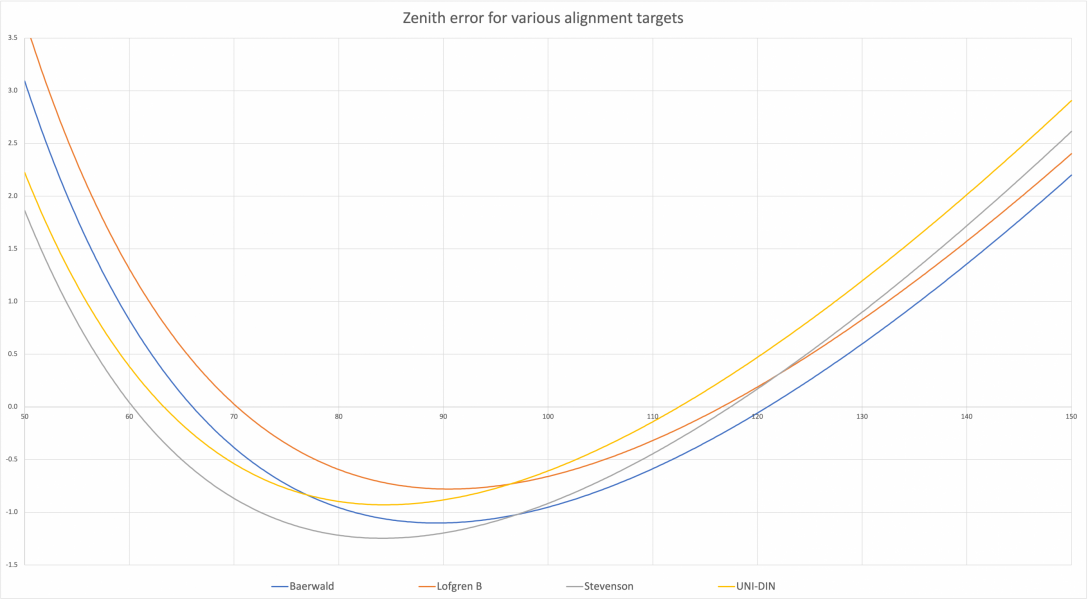
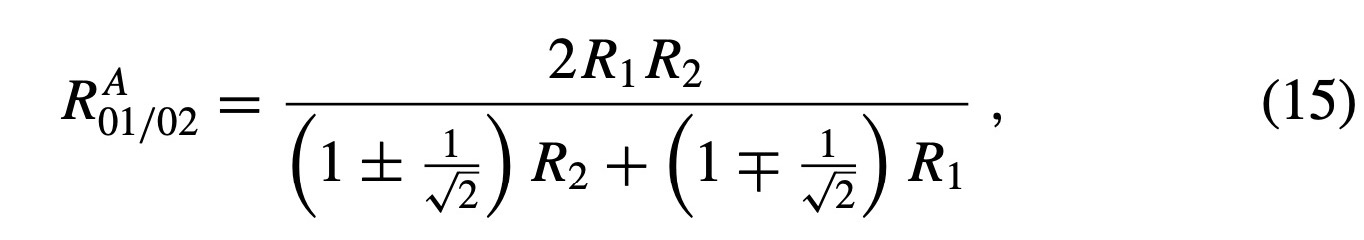Like I said previously, the “design goal” is where I want the least distortion - which would be exactly zero at the null points but non-zero elsewhere. There’s absolutely nothing magical here. If I change the null point slightly I will get a slightly different zenith error at a given radius. ALL of this is in accordance to the formulas posted above.No, they are not chosen arbitrarily when it comes to Lofgren A, B, Stevenson or UNI-DIN. Those null points are chosen in order to reach design goals of each geometry over the recorded area of vinyl record. The limits of the recorded area is determined by the standard (IEC, DIN, JIS) which inevitably changes null points.
Everybody agrees on this but you don't. It is unbelievable to see you still arguing. Please do some research.
Just try the exercise I suggested and you will see. I just did for the kicks of it. I took the table you posted above, and calculated the two null points according to the formula:
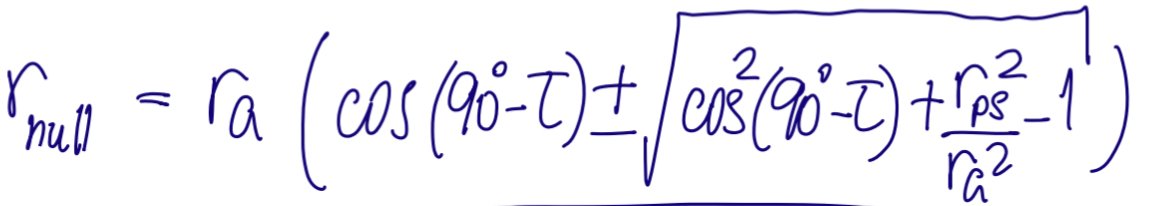
and compared it to the null points in the table. Within 0.0x mm they tie out in every case.
Please make sure that the appropriate angle conversions are used or your results will be wrong. For example my Excel’s “cos” assumes angles in radians, so the argument for the null points calc should be (90-tau)*Pi/180, not 90-tau.
Last edited: