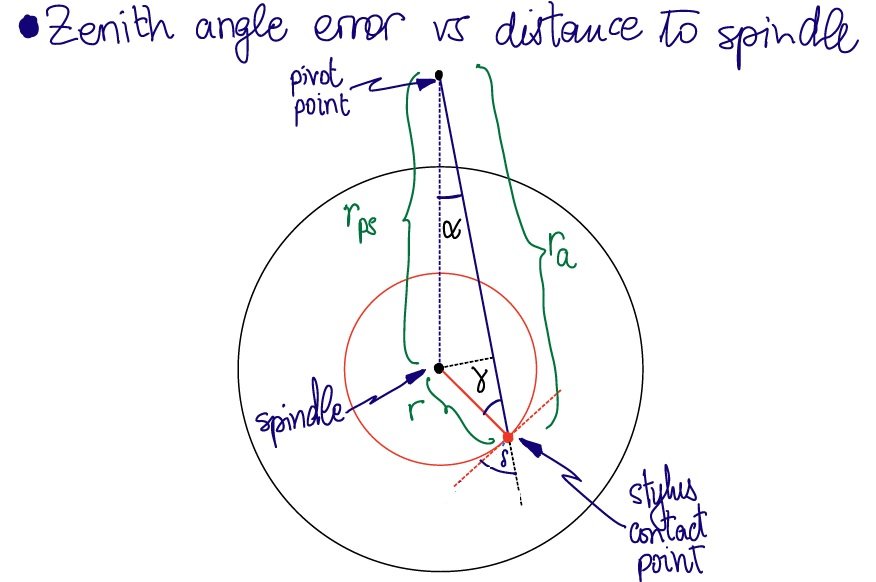
RE: "The math I started this thread with shows the zenith error for a given pivot-spindle and overhang" in the initial case when there is no headshell offset T (pic attached), my read of this is (a) the ra, headshell, cart body, and cantilever are all collinear and hence (b) at this point the delta is the traditional tracking error?Couple of points:
The math I started this thread with shows the zenith error for a given pivot-spindle and overhang. The shape of that function is given with these two numbers. When you introduce the offset angle ("Tau" in the formula) you move that function up and down on the plot, and doing so changes where the null points are.
But the point remains is: you can choose Baerwald, Lofgren B, etc and that will change the places where you have the nulls. You might need to change overhang to match both points. But after all this, you still have an angle variation of about 2.5 degrees give or take, the choice is just where to make this smaller, but those choices are fairly subtle.
What you see with AnalogMagik is that getting the zenith of the stylus, not the cantiliver, right is key. You can get a large improvement in the IMD with just a 1/2 degree adjustment. If you align with your cantilever, and you don't use AM (or possibly using Wally's optical analysis), your zenith will be off almost surely.
As for the quality of the pressing, for most parameters (eg azimuth and zenith), all you need to check was done right is the lacquer, not every pressing. I am pretty sure AM has put a lot of effort in verifying their cutter head was aligned and working correctly.
Ultimately, the proof is in the listening, and I can tell you record after record, getting zenith right makes a huge difference.
This delta would also be the first choice for an offset angle adjustment if there were no zenith issues?
If the cartridge was manufactured accurately, the stylus tip's leading edge/face will be facing "forward" wrt the cart and will have no zenith (swivel) error. If manufacturing was not spot on, there could be some zenith error, due to rotation of the stylus tip about its core axis, which would compound tracking issues.
The final first phase (before T is introduced) formula for delta as a function of r (with important constants P2S length and OH length implicit in ra) is instructive. It visually shows that anyone could experiment with logical pairs of null points (without any reference to first or last modulated grooves,). One just has to set delta to zero and solve the quadratic in r for two values.
The maths are presented very clearly and a pleasure to digest, but am I correct in how I am reading the situation represented by/after the introduction of headshell offset T. Is this the major adjustment, leaving B to be just the residual fine-tuning real zenith error (misoriented stylus tip on a cantilever)? If we can solve for the null point r+ and r- now by just setting B =0, that means we must have eliminated all other tracking error at this point. All we did in phase two was introduce (apply) T to the cartridge in the headshell, so T must be the traditional offset (excluding the finesse of zenith error fix)? If my read is okay, I understand everything I read and feel good
(afterthought: I believe the x = ra*sin(alpha) should be = rps *sin(alpha) and y = rps - ra*cos(alpha) should be = ra - rps *cos(alpha). No impact on major equation (1) as sin^2 + cos^2 =1 either way in the expansion process.)
Afterthought to my T question. I see in the calculations both "if the was no offset angle in the headshell" and "introducing a headshell offset angle". The first sounds like an orientation of cartridge within and relative to the headshell. The second sounds like a reference to an angled headshell. Small point but just wanted to sure if the situation was a user adjustment (variable) or a constant associated with (non straight) tonearm design? Tnx
Attachments
Last edited: