Interconnects between SS and valve components

[bonzo75]

I am quite sure if I use a valve pre to drive an SS amp it will be VTL (low impedance high current) which Marty uses successfully with spectral, NAT, ypsilon, or CAT (because it is naturally mated with symphonic line Kraft). That still does not answer the question will ICs matter more.

My Lampi to SS pre question is that i find the valve pre amps are slower than the Lampi (though they have some positives), and for the sake of power amp pre amp synergy, it might be worth trying a quality SS pre, in which case the IC from Lampi to pre question stands

 

[bonzo75]

+1 to the "it´s more complicated than ..." ! The old x10 rule has more exceptions than applications. Most modern tube preamplifiers have relatively low output impedance but some of them do not like supplying current as you say, although they can do it.

A significant number of solid state amplifiers have input impedance over 50 kohm. And we have reported cases of people using Burmester amplifiers (input impedance around 2K ) with Audio Research tubed preamplifiers with great success, something I could never understand ...

I don't get how that tonepub guy uses audio research for that purpose either

 

[DaveC]

Where were we putting it directly to amps? The question is for Lampi into pre, or valve pre into SS power, does IC matter more?

Sujay is running his Lampi into his Burmester

Yes, it could be a preamp or an amp as there is a VC option on Lampis so a pre is optional. Either way, you have to be careful about the device the Lampi is driving as it is not compatible with everything.

 

[bonzo75]

Yes, it could be a preamp or an amp as there is a VC option on Lampis so a pre is optional. Either way, you have to be careful about the device the Lampi is driving as it is not compatible with everything.

Yes my Lampi does not have that pre option to drive amps

 

[bonzo75]

Maybe I should re phrase the question. Let's say the components are compatible with each other. Will changing IC matter more while connecting one valve and one SS than with two valves and two SS. Have people had these experiences where their cables mattered more in such cases

 

[DaveC]

I am quite sure if I use a valve pre to drive an SS amp it will be VTL (low impedance high current) which Marty uses successfully with spectral, NAT, ypsilon, or CAT (because it is naturally mated with symphonic line Kraft). That still does not answer the question will ICs matter more.

My Lampi to SS pre question is that i find the valve pre amps are slower than the Lampi (though they have some positives), and for the sake of power amp pre amp synergy, it might be worth trying a quality SS pre, in which case the IC from Lampi to pre question stands

Most preamps aren't as nice sounding as the Lampi DHT output section. I'd use a high quality SS pre myself, check out PranaFidelty, the preamp Steven makes is exceptionally good... very transparent, resolving and neutral with adjustable gain.

IC cables always matter and are always critical. How much they might matter is just speculation...

 

[DonH50]

I was enjoying these complicated impedance matching questions from afar . . . until I realized that I may be going from tube to solid-state to tube and therefore I have a whole impedance matching analysis to undertake!

1) The output impedance of the Io preamp is 350 ohms. The Io might be driving a solid-state amplifier with an input impedance of 10,000 ohms. Is this OK?

2) The solid-state amplifier is built into a bass tower and drives its attached cones. This built-in amplifier has a passive high-pass filter which sends the midrange and treble frequencies to VTL MB-750s. I do not know the output impedance of the amplifier. (It probably is low.) The MB-750 has an input impedance of 130,000 ohms. Is this OK?

Agree with Dave FWIW.

Assuming the preamp has low enough distortion into a 10 k load, it is about 0.3 dB attenuation, negligible in this application. A lot of high-Z tube circuits only have around 1 ~ 3 mA of drive current so cannot tolerate a small'ish load. A cathode-follower buffer is usually biased a little hotter than that, and in any event 1 Vrms across 10 k ohms is only 100 uArms, so you should be OK.

No problems at all for SS driving 130 k ohms. If the passive filter is not buffered it's frequency response will change with the source and load but the min load (and source) impedances should be specified. I doubt there's any problems there.

I'll bow out, seems like I led this thread astray of the OP's intent (need to quit posting here unless it is in the technical area, sorry guys). - Don

 

[Ron Resnick]

Agree with Dave FWIW.

Assuming the preamp has low enough distortion into a 10 k load, it is about 0.3 dB attenuation, negligible in this application. A lot of high-Z tube circuits only have around 1 ~ 3 mA of drive current so cannot tolerate a small'ish load. A cathode-follower buffer is usually biased a little hotter than that, and in any event 1 Vrms across 10 k ohms is only 100 uArms, so you should be OK.

No problems at all for SS driving 130 k ohms. If the passive filter is not buffered it's frequency response will change with the source and load but the min load (and source) impedances should be specified. I doubt there's any problems there.

I'll bow out, seems like I led this thread astray of the OP's intent (need to quit posting here unless it is in the technical area, sorry guys). - Don

Thank you for weighing in, Don. I appreciate it!

I, for one, like your posts whether they are technical or non-technical.

With respect to your comment about the passive filter, by "load" do you mean the amplifier which is receiving the high-pass signal? If that is the case then isn't the "load" the VTL with an input impedance of 130Kohm?

By "source" of the passive filter do you mean the output of the Io?

 

[bonzo75]

I'll bow out, seems like I led this thread astray of the OP's intent (need to quit posting here unless it is in the technical area, sorry guys). - Don

Don, appreciate your insight, please do continue posting on the thread.

 

[DonH50]

@bonzo75: OK, thanks, I thought by your comments you were only (or primarily) interested in listening impressions and I don't really have any to offer that would mean anything (not current with high-end cables). If there is cable sensitivity, I would expect SS-SS to exhibit the least impact, then SS-V/V-SS, and finally V-V the most sensitive to the cable where SS = solid-state and V = valve (instead of "tube" seeing as how you are on the other side of the pond from me ). That is based on the typical impedances and of course YMMV with specific components and all that jazz.

Thank you for weighing in, Don. I appreciate it!

I, for one, like your posts whether they are technical or non-technical.

With respect to your comment about the passive filter, by "load" do you mean the amplifier which is receiving the high-pass signal? If that is the case then isn't the "load" the VTL with an input impedance of 130Kohm?

By "source" of the passive filter do you mean the output of the Io?

Thanks Ron.

Yes.

A passive filter to me means a simple RLC (resistor, inductor, capacitor) design with no active components. That means no buffers at its input or output to isolate the filter from whatever drives it (its source) and whatever it is driving (its load). Consider a simple single-pole LPF comprising a single RC as shown in the figure. A capacitor goes from infinite impedance at DC to a short at very high frequencies so that is what causes the frequency roll-off. The corner (roll-off) frequency is 1 / (2 * pi * Rlpf * Clpf) assumming the source (driving) impedance Rin is 0 ohms (an ideal voltage source) and the load impedance Rload is infinite (an open circuit). Aside: in the real world impedances are more than simple resistors but they are fine for this example.



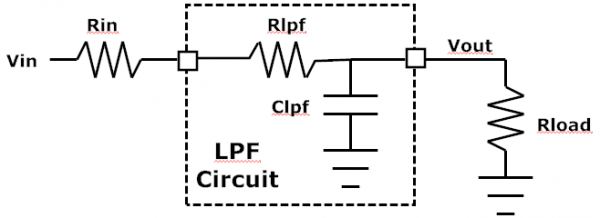
The equation for the filter’s transfer function with ideal (0-ohm Rin) source and load (infinite Rload) is:

Vout/Vin = 1 / (1 + s*Rlpf*Clpf) where s is the complex frequency value:
s = jw = j*2*pi*f; w = freq in radians/s, f = freq in Hz, j = sqrt(-1)

Clearly if the source resistor is not 0 ohms, then the total series resistance is higher (Rin + Rlpf > Rlpf alone) and the corner frequency will drop. If the load resistance is not infinite it will do a couple of things: it will reduce (attenuate) the output because of the voltage divider formed by (Rin + Rlpf) and Rload, and it changes the frequency response. The equation when the load is finite (instead of infinite) is:

Vout/Vin = Rload / (Rlpf + Rload + s*Rlpf*Rload*Clpf)

If Rload is infinite this devolves to the same equation as above. The net result is that finite but high load impedance changes the gain (attenuation) and frequency of the LPF a little bit. Active buffers are designed to present a high impedance to the source (Vin) and low output impedance to the filter, and on the output presents a high-impedance load to the filter and low-impedance driving source to the next component in the chain. Without them, the LPF (or whatever type passive filter is used) is more sensitive to whatever drives and loads it. In the real world a decent passive filter will accommodate a pretty wide range of source and load impedances without significantly changing the filter’s frequency response.

HTH - Don