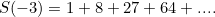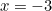.
Infinity is fine for mathematicians. They can deal with abstractions.
Infinity is a nightmare for physicists. They have to deal with the concrete world.
question for computer people or mathematicians:
Can a presently available computer deal with numbers as great as ten to the billionth power as a possible substitute for infinity?
Infinity is fine for mathematicians. They can deal with abstractions.
Infinity is a nightmare for physicists. They have to deal with the concrete world.
question for computer people or mathematicians:
Can a presently available computer deal with numbers as great as ten to the billionth power as a possible substitute for infinity?
Last edited: